LDA 란?

• LDA 의 목표는 어떤 새로운 데이터가 주어졌을 때, 어떤 클래스에 속하는지 에측하는 것.
  • 우선 예측변수가 1개인 경우
• 그럼 예측변수(predictor variable) 란 무엇인가? 데이터가 가진 특징을 의미한다. 어떤 사람의 키(cm)나 몸무게(kg)가 에시가 될 수 있다.
• 클래스란 우리가 예측하고 싶은 카테고리를 의미한다. 키에 따라 사람을 Class1(청소년), Class2(중년)로 나누고 싶다고 하자.

• 위 같은 데이터를 보고 새로운 사람의 키(예측변수 x) 가 주어질 때, 이 사람이 어느 클래스에 속하는지(청소년 / 성인)를 맞추는 것이 목표다.

그래서 LDA 가 하는 일은?

• 청소년의 키는 대체로 150 ~ 160cm, 성인의 키는 대체로 170 ~ 180cm 일 때, 둘 다 각각의 가우스 분포를 가정하고, 그걸 바탕으로 새로운 키에 확률을 게산해서 더 높은 확률이 나오는 클래스를 선택하는 것.
• 정리 : 위 예시에서는 예측변수가 키 하나이기 때문에 p = 1 일 때 선형판별분석(LDA) 을 한다.

다시 LDA for p = 1 정리

• LDA 의 핵심 가정은 각 클래스의 데이터 분포는 정규분포(가우시안 분포)를 따른다고 가정한다.

• 그리고 모든 클래스의 분산(σ²) 은 동일하다고 가정.

• 이를 수식으로 표현하면 아래와 같다.

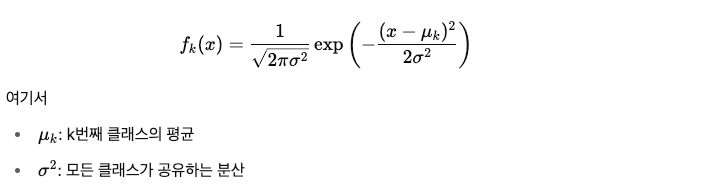
• 클래스 구분 방법 (분류 과정) 은 다음과 같다.

1. 각각의 클래스마다 fk(x) 을 계산한다.
2. 베이즈 정리를 이용해 후험확률 pk(x) 를 계산
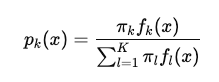
3. pk(x) 가 가장 큰 클래스로 분류. 로그를 취해서 계산을 단순화하면 관측값 x 를 다음을 최대화하는 클래스에 할당하는 것과 같다. 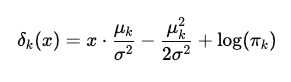여기서 𝛿𝑘(𝑥) 는 일종의 점수(score) 로 보고, 가장 점수가 큰 클래스를 선택하면 된다. 이 식이 x 에 대해 선형이기 때문에 Linear Discriminant Analysis 가 된다.

쉽게 예를 들어, 두 클래스가 있고 각각 평균이 다르지만 분산은 같다면

• 두 클래스의 평균을 딱 중간에 나눈 값이 경계선이 된다.
• 예를 들어, 클래스 1 평균이 -1, 클래스 2 평균이 +1 이면, 경계는 0이 된다.
  • 예측 변수 x 가 0보다 작으면 클래스1, 크면 클래스2로 분류 할 수 있다.

LDA for p = 1 요약

• LDA for p=1은 "한 개의 변수로 정규분포를 가정하고" "가장 확률 높은 클래스로 분류"하는 방법.
• 핵심 포인트: 모든 클래스의 분산은 같다고 가정, 그리고 식이 x에 대해 선형이라 계산이 간단!